What is fuzzy logic?
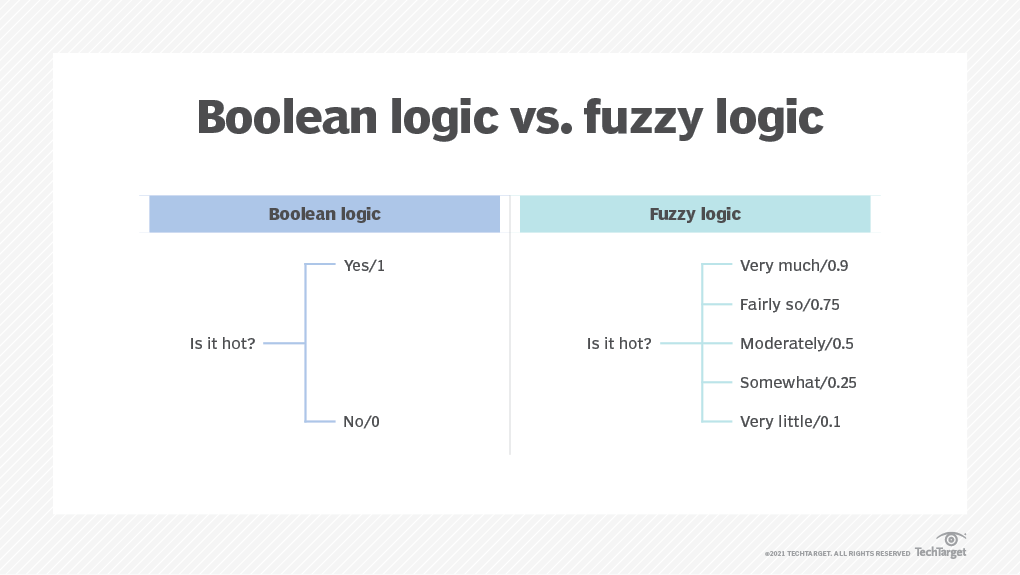
Fuzzy logic is an approach to computing based on "degrees of truth" rather than the usual "true or false" (1 or 0) Boolean logic on which the modern computer is based.
The idea of fuzzy logic was first advanced by Lotfi Zadeh of the University of California at Berkeley in the 1960s. Zadeh was working on the problem of computer understanding of natural language. Natural language -- like most other activities in life and indeed the universe -- is not easily translated into the absolute terms of 0 and 1. Whether everything is ultimately describable in binary terms is a philosophical question worth pursuing, but in practice, much data we might want to feed a computer is in some state in between and so, frequently, are the results of computing. It may help to see fuzzy logic as the way reasoning really works and binary, or Boolean, logic is simply a special case of it.
Fuzzy logic in AI
In artificial intelligence (AI) systems, fuzzy logic is used to imitate human reasoning and cognition. Rather than strictly binary cases of truth, fuzzy logic includes 0 and 1 as extreme cases of truth but with various intermediate degrees of truth.
As a result, fuzzy logic is well-suited for the following:
- engineering for decisions without clear certainties and uncertainties, or with imprecise data -- such as with natural language processing technologies; and
- regulating and controlling machine outputs, according to multiple inputs/input variables -- such as with temperature control systems.
IBM's Watson supercomputer is one of the most prominent examples of how variations of fuzzy logic and fuzzy semantics are used.
 How fuzzy logic is used in technology
How fuzzy logic is used in technology
Fuzzy logic applications
Various types of AI systems and technologies use fuzzy logic. This includes vehicle intelligence, consumer electronics, medicine, software, chemicals and aerospace.
- In automobiles, fuzzy logic is used for gear selection and is based on factors such as engine load, road conditions and style of driving.
- In dishwashers, fuzzy logic is used to determine the washing strategy and power needed, which is based on factors such as the number of dishes and the level of food residue on the dishes.
- In copy machines, fuzzy logic is used to adjust drum voltage based on factors such as humidity, picture density and temperature.
- In aerospace, fuzzy logic is used to manage altitude control for satellites and spacecrafts based on environmental factors.
- In medicine, fuzzy logic is used for computer-aided diagnoses, based on factors such as symptoms and medical history.
- In chemical distillation, fuzzy logic is used to control pH and temperature variables.
- In natural language processing, fuzzy logic is used to determine semantic relations between concepts represented by words and other linguistic variables.
- In environmental control systems, such as air conditioners and heaters, fuzzy logic determines output based on factors such as current temperature and target temperature.
- In a business rules engine, fuzzy logic may be used to streamline decision-making according to predetermined criteria.
WHAT IS FUZZY LOGIC?
The concept of fuzzy logic was introduced by Lotfi Zadeh of the University of California, Berkeley, in the 1960s.3 Zadeh was working on the problem of helping computers understand natural language, which, like many other human activities, is not easily translated into absolute terms of 0 and 1. (Whether everything is ultimately describable in binary terms is a philosophical question worth pursuing. In practice, much of the data we might want to feed into a computer exists in in-between states. The same frequently applies to the results of computing.) It may help to see fuzzy logic as the way human reasoning normally works, with binary and Boolean logic as special cases.
In fuzzy logic, 0 and 1 are extreme cases of truth (or fact) and encompass various states of in-between truth, so that, for example, at 72 inches, or six feet, a man’s height would not be “tall” or “short” but “25 percent of tallness,” with a 0.25 membership grade. The concept of membership grade is important in fuzzy logic, quantifying where a single data point lies within a fuzzy set, in which 0 means it is not a member of that set and 1 that it is fully a member.
Fuzzy logic seems closer to the way our brains actually work. We aggregate data and form a number of partial truths that we aggregate further into higher truths, which, when certain thresholds are exceeded, trigger results such as motor reactions. A similar kind of process can be found in neural networks, expert systems and other AI applications. Fuzzy logic is essential to the development of humanlike capabilities for AI, sometimes referred to as artificial general intelligence: the representation of generalized human cognitive abilities in software so that the AI system can find a solution when it faces an unfamiliar task.
WHY FUZZY LOGIC?
In all domains, from marketing to engineering, we need to deal with uncertainty in order to solve problems and make decisions. Fuzzy logic is a system that helps us do all of these things better by programming machines to think as humans do. It may not give us accurate reasoning, but it provides us with acceptable reasoning.
Fuzzy logic accepts that we are unable to provide a precise number for many uncertainties in life. Information is often imperfect, and data has errors. By replacing binary either/or options with if/then possibilities, fuzzy logic expands choices and considers subjective attributes.
The basis of fuzzy logic is also the basis of human communication. Because fuzzy logic is built on structures of qualitative description used in everyday language — what’s known as linguistic variables, such as “short,” “medium” or “tall” in the height example — it is easier to understand. Moreover, because the mathematical concepts behind fuzzy reasoning are relatively simple, it represents an intuitive approach without far-reaching complexity.
A fuzzy logic system can be defined as the nonlinear mapping of an input dataset to scalar output data, a consequence of Zadeh’s initial algebra.4 Such a system consists of four main parts: a fuzzifier, a set of rules, an inference engine and a defuzzifier.

The common fuzzy logic system processes data in three sequential stages: fuzzification, inference and defuzzification. In the fuzzification step, a crisp, or well-defined, set of input data is gathered and converted to a fuzzy set using fuzzy linguistic variables — that is, fuzzy linguistic terms. Second, an inference is made based on a set of rules. Last, in the defuzzification step the resulting output is mapped using so-called membership functions. A membership function is a curve that maps how each point in the input space is related to a membership grade. Using the height example, various heights in a given set would receive a membership grade between 0 and 1; the resulting curve would not define “tall” but instead would trace the transition from not tall to tall.
PRACTICAL APPLICATIONS OF FUZZY LOGIC
Fuzzy logic was initially used in control systems such as camera lenses. Today it lies behind many mechanical systems we take for granted. For example, in a conventional air conditioner controller, the thermostat compares the temperature the user selects on the dial with the actual room temperature and turns the AC on or off. This maintains a certain temperature level. However, the actual room temperature does not always correspond to the subjective temperature felt by people in the room. Empirical analysis of how people adjust the temperature dial on air conditioners shows a number of tendencies:
- People tend to put the temperature dial lower than necessary, then forget to turn it up again, wasting energy.
- If someone changes the temperature regularly, the temperature control should be sensible — that is, the AC controller should react more quickly.
- Room temperature that varies a lot suggests the room is used a lot. Hence, control should be sensible.
There’s another variable to consider. Regularly turning the AC on or off will shorten the life of the device and cause ineffective energy usage. To prevent this from happening, air conditioner manufacturers make use of a temperature band called hysteresis — the tendency of the value of a physical property to lag the force creating it — between the on and off operations. A large hysteresis will cause the temperature at which the output changes from off to on to be lower than the set point by the amount of the hysteresis. If the hysteresis is small, the output will change near the set point, making the temperature control more responsive. Thus, the hysteresis needs to have a suitable value.
Because this kind of knowledge is difficult to model mathematically or code in a conventional algorithm, fuzzy logic has been used. The fuzzy logic system corrects the signal before the set point is reached and sets its hysteresis. To accomplish this, the system uses three input variables:
- The difference between the set temperature and the actual room temperature. When this difference is large, the system boosts the signal so that the desired temperature is reached faster (see Table 1, Rules 1 and 2) and sets the hysteresis to large so minor disturbances do not cause unnecessary on/off switches.
- The number of set temperature changes. To satisfy users who try to set the room temperature very precisely (Rule 3), the hysteresis is set to small.
- The brightness. When lights are on and the brightness is at a medium level, the temperature is set slightly higher (Rule 4) and the hysteresis is set lower. If the room is hit by direct sunlight, the set temperature is automatically reduced (Rule 5).

Table 1 shows the rule base that defines the strategy of the AC system. Each row represents a rule. The left column under “If” shows all input variables of the rules; the right column under “Then” shows all the output variables.
In this rule base, each linguistic label, such as “too cold,” “too warm,” “frequent,” “medium” or “high,” is represented by a predefined membership function.
FUZZY LOGIC IN AUTONOMOUS VEHICLES
Air conditioners are relatively straightforward. In autonomous vehicle control systems, however, a large number of embedded systems interact with one another with the aim of controlling a car without the involvement of a human driver. Despite the complexity of this task, some car manufacturers have made considerable progress in autonomous systems, although development programs continue. Recently, Tesla introduced Autopilot, which can take full control of the vehicle’s steering wheel, throttle and brakes. Alphabet’s Google and Uber Technologies have also been testing self-driving cars. Typically, there are three important modules in a self-driving car: speed control, steering-wheel control and adaptive cruise control. We will outline the design of the speed control module with a fuzzy logic system that has three input variables — speed, range of view and road quality — and two output variables: throttle and brake.
Step 1: Fuzzification
Membership functions allow us to graphically represent a fuzzy set. These functions can assume specific shapes, such as triangular, trapezoidal, piecewise linear, Gaussian or singleton, and help represent the degree of truth in the valuation process of particular phenomena where multiple answers are possible. The type of membership function is dependent on context and is generally chosen according to the user’s experience or the nature of the data. In our example, we choose the triangle shape to express the membership functions of fuzzy sets, seen in Figures 2 through 6.
Each of these linguistic variables — speed, range of view, road quality and the level of braking and throttle — have corresponding linguistic values; for example, speed can be low, average or high, as in Figure 2. Each linguistic value is a fuzzy set with a membership function showing the membership grade of each value in the universe of discourse of the fuzzy set.
In this case, the membership functions for input and output variables are generated either from recommendations from experts such as automobile engineers or through clustering methods. More specifically, as we see in Figure 2, we have three linguistic labels of speed: low, average and high. For each crisp value of volatility along the x-axis, we may get its membership grade in corresponding fuzzy sets by taking the corresponding y-axis values. Note that an important characteristic of fuzzy logic is that a numerical value does not have to be fuzzified using only one membership function. In other words, a value can belong to multiple sets at the same time. In Figure 3, a range-of-view value of 12.5m can be considered both “low” and “average” at the same time, with different degrees of membership, at 0.25 and 0.75, respectively.

Step 2: Constructing Knowledge-Based Rules
Like the thermostat, a speed-control module for self-driving cars requires a rules base to control the output variable. A fuzzy rule is a simple “if–then” rule with a condition and a conclusion. For instance, if speed is high, range of view is low and road quality is rough, then the brake is average. Experts or training data can provide these rules or you can extract rules from the data itself, through clustering methods. The fuzzy rules in this example are listed in Table 2.

Each rule shows how the speed-control module reacts when input variables such as speed, range of view and road quality take on certain values. For instance, Rule 2 can be read as follows: If the car is moving fast, the range of view is low and the road is rough, then the system will brake with average force.
Step 3: Inference
The purpose of this step is to map a given input to an output using knowledge-based rules and fuzzy set operators.
Fuzzy set operators
After inputs are fuzzified, we can determine the degree to which each part of the antecedent is satisfied for each rule. (The antecedent is the “if” part of the rule.) If the antecedent of a given rule has more than one part, the fuzzy operator is applied to obtain a number that represents the result of the antecedent for that rule. This number is then applied through a fuzzy operator to the output function — a process known as implication. The input to the fuzzy operator is two or more membership values from fuzzified input variables. The output is a single truth value. Fuzzy set operators can also be used to combine the results of individual rules.
The rules in fuzzy logic are usually “If A and/or B, then C,” which means that we need to define operators “and” and “or.” The most commonly used fuzzy operators for “or” and “and” are max and min, respectively, which Zadeh proposed in the early years of his work on fuzzy logic.
Figure 2, Figure 3 and Figure 4 show the operator min at work, evaluating the antecedent for a brake-decision calculation involving Rule 2: If speed is high, range of view is low and road quality is rough, then brake is average. The given numeric inputs are speed = 70 miles per hour, range of view = 12.5, road quality = -0.4. The three different pieces of the antecedent yield fuzzy membership values of 0.75, 0.25 and 0.8, respectively. The fuzzy “and” operator selects the minimum of the three values, 0.25, and the fuzzy operation for this rule is complete.
Fuzzy inference
Every rule has a weight (between 0 and 1), which is applied to the value of the antecedent. To make it simple, we choose the weight of 1, which has no effect at all on the implication process.
A consequent is a fuzzy set represented by a membership function, which is reshaped using a function associated with a number representing the antecedent. The input for the implication process is the antecedent value, and the output is a fuzzy set. Implication is implemented for each rule and then combined into a single fuzzy set to make a decision for the final output, a process called aggregation. The input of the aggregation process is the list of output functions generated by the implication process for each rule. The output of the aggregation process is a fuzzy set for each output variable. The whole process — from crisp inputs, implications of all rules and aggregation — is called fuzzy inference.
Step 4: Defuzzification
The input for the defuzzification process is a fuzzy set (the aggregate output fuzzy set), and the output is a single number. However, the aggregation output encompasses a range of output values, which must be defuzzified in order to produce a single output value for the set. This is the purpose of the defuzzifier component of a fuzzy logic system.
For example, assume that inference provides the result in Figure 7. The shaded area belongs to the output fuzzy result. The goal is to obtain a single crisp value. There are a number of different methods of defuzzification, such as the center of the area, center of sums, center of maximum and mean of maximum. Perhaps the most popular defuzzification method is the center of the area. The star, with the value 0.35, shows the level of braking applied to the wheels in a specific context.

CONCLUSION
Because of the rapid development of modern information technologies, it is possible today to collect, store, transfer and combine huge amounts of data at relatively low costs. However, exploiting the information contained in those data archives in an intelligent way turns out to be difficult. In knowledge discovery and data mining, there is a tendency to focus on purely data-driven approaches. However, in order to get truly useful results, we must take into account background knowledge, non-numeric information and uncertainties, and we must focus on comprehensible models. Fuzzy logic helps to make a link between traditional knowledge-driven approaches and purely data-driven ones because aspects of knowledge representation and reasoning have dominated research in fuzzy set theory for some time.
Fuzzy logic, with its ability to handle uncertainties, has been widely applied to many engineering and scientific tasks. The examples of the air-conditioner controller and the speed-control module in a self-driving car show us how fuzzy logic can be applied to systems in which information and noise go hand in hand. The inputs of the speed-control system are actually crisp numbers that are then fuzzified into fuzzy sets. Rules are derived that show hidden relationships within the input data. These rules are used in an inference module to generate the output, which is a fuzzy set. To produce the final output as a crisp number, the fuzzy set output then undergoes defuzzification to a single value.
All in all, fuzzy logic is not only a theory but another way to look at the world. Fuzzy logic presents practical ways to solve many problems in various fields. The answer does not always require complicated equations; sometimes it just needs some common sense and a little fuzzy thinking.
ENDNOTES
1. A. Zadeh. “Fuzzy Sets.” Information and Control 8, no. 3 (1965): 338-53.
2. Eyke Hüllermeier. “Does Machine Learning Need Fuzzy Logic?” Fuzzy Sets and Systems281 (2015): 292-99.
3. “Fuzzy Control Programming, Technical Report.” International Electrotechnical Commission (1997).
4. Jerry M. Mendel, “Fuzzy Logic Systems for Engineering: A Tutorial,” Proceedings of the IEEE 83, no. 3 (1995):345-77.
https://www.weareworldquant.com/en/thought-leadership/reshaping-the-world-with-fuzzy-logic/
Percentage of Membership vs Degrees of Membership;
What is Being Young or Old in Fuzzy Logic?
At this juncture it is important to point out the distinction between fuzzy systems and probability. Both operate over the same numeric range, and at first glance both have similar values: 0.0 representing False (or non-membership), and 1.0 representing True (or membership).
However, there is a distinction to be made between the two statements: The probabilistic approach yields the natural-language statement, "There is an 80% chance that Jane is old," while the fuzzy terminology corresponds to "Jane's degree of membership within the set of old people is 0.80." The semantic difference is significant: the first view supposes that Jane is or is not old (still caught in the Law of the Excluded Middle); it is just that we only have an 80% chance of knowing which set she is in. By contrast, fuzzy terminology supposes that Jane is "more or less" old, or some other term corresponding to the value of 0.80. There are more very technical ways to show how comparing probibility with fuzzy degrees of truth and falsehood don't match.
Natural language abounds with vague and imprecise concepts, such as "Sally is tall," or "It is very hot today." Such statements are difficult to translate into more precise language without losing some of their semantic value: for example, the statement "Sally's height is 152 cm." does not explicitly state that she is tall, and the statement "Sally's height is 1.2 standard deviations about the mean height for women of her age in her culture" is fraught with difficulties: would a woman 1.1999999 standard deviations above the mean be tall? Which culture does Sally belong to, and how is membership in it defined?
While it might be argued that such vagueness is an obstacle to clarity of meaning, only the most staunch traditionalists would hold that there is no loss of richness of meaning when statements such as "Sally is tall" are discarded from a language. Yet this is just what happens when one tries to translate human language into classic logic.
"To what degree is something true or false?"
)) There are two types of thinking:
)) Approximate and Exact.
Exact is just a "degree of truth" equal to 100%. Approximate is a degree of truth between 1% and 99%. Therefore there is only one type of thinking: Fuzzy Think!
)) Approximate always trumps Exact.
Unlike traditional or classical logic, which attempts to categorize information into binary patterns such as black / white, true / false, yes / no, or all / nothing, Fuzzy Logic pays attention to the "excluded middle" and tries to account for the "grays", the partially true and partially false situations which make up 99.9% of human reasoning in everyday life. It builds upon the assumption that everything consists of degrees on a sliding scale-whether it be truth, age, beauty, wealth, color, race, or anything else that is effected by the dynamic nature of human behavior and perception. The question Zadeh always insists upon asking is, "To what degree is something true or false?"
Zadeh looks around him in the real world which he finds pervaded by concepts which do not have sharply defined boundaries, where information is often incomplete or sometimes unreliable. In fact, he would classify most words as having fuzzy meanings-virtually every adjective or adverb in ordinary speech. These concepts become clear if seen in transition from membership to non-membership in gradual, rather than abrupt, increments.
In quest for precision, scientists have generally attempted to manipulate the real world into artificial mathematical models that make no provision for gradation. They have tried to describe the laws governing the incredibly complex behavior of humans, both singly and in groups, in mathematical terms similar to those employed in the analysis of inanimate systems, which, in Zadeh's view, has been, and will continue to be, a misdirected effort.
Because the human mind can't handle so many isolated separate ideas at one time, it tends to bundle similarly-related objects into categories in such a way as to reduce the complexity of the information processing task. It is this incredible capacity of the human mind to manipulate these fuzzy or unsharp categories that distinguishes human intelligence from the machine intelligence of current generation computers.
Because Fuzzy Logic provides the tools to classify information into broad, coarse categorizations or groupings, it has infinite possibilities for application which have proven to be much cheaper, simpler and more effective than other systems in handling complex information. Fuzzy Logic has extremely broad implications for many fields not just electrical engineering and computer technology which have been fairly quick to incorporate its theoretical principles. Numerous consumer goods especially household products and electronic equipment-microwaves, cameras, and camcorders already incorporate Fuzzy Logic into their design. So have computer control systems such as the famous subway of Sendai, Japan, or numerous complex diagnostic and monitoring biomedical systems which are starting to be used in hospitals.
But other fields such as the social sciences-economy, finance, psychology, sociology, politics, religion, ethics, law, medicine, geography, folklore, anthropology that deal with the complexity of human behavior-are just beginning to explore the infinite possibilities of Fuzzy Logic.
Zadeh was not the first to think about "shades of gray". Philosophers such as Plato indicated that there was a third region (beyond "true" and "false") where opposites "tumbled about". Hegel, Marx, Engels and Lukasiewicz, among others, also dealt with middle regions. But it was Zadeh who first developed the general theory and laid the foundation for what Fuzzy Logic is today.
For a well-researched, very readable, popular description of Lotfi Zadeh and the development of the field of Fuzzy Logic, refer to Daniel McNeill and Paul Freiberger's award winning book, Fuzzy Logic: The Revolutionary Computer Technology that is Changing our World, 1993. For a technical introduction to the field, see Zadeh's Fuzzy Sets and Applications: Selected Papers. Edited by Yager, Ovchnikov, Tong, and Nguyen. New York: Wiley, 1987.
http://www.google.com/search?hl=en&q=Zadeh+fuzzy+logic
What is being Tall or Short in Fuzzy Logic?
The real world simply doesn't map well to binary distinctions, and numerical precision is often unhelpful in making qualitative statements. Fuzzy logic gives us a way to deal with such situations.
In fuzzy systems, values are indicated by a number (called a truth value) in the range from 0 to 1, where 0.0 represents absolute falseness and 1.0 represents absolute truth. While this range evokes the idea of probability, fuzzy logic and fuzzy sets operate quite differently from probability.
If I tell you that my height is 5 ft. 6 in. (or 168 cm), you may have to think a bit before deciding whether you consider me short or not short (i.e., tall). Moreover, you might reckon me short for a man but tall for a woman. So let's make the statement "Russell is short," and give that a truth value of 0.70.
If 0.70 represented a probability value, we would read it as "There is a 70% chance that Russell is short," meaning that we still believe that Russell is either short or not short, and we have a 70% chance of knowing which group he belongs to. But fuzzy terminology really translates to "Russell's degree of membership in the set of short people is 0.70," by which we mean that if we take all the (fuzzy set of) short people and line them up, Russell is positioned 70% of the way to the shortest. In conversation, we would say Russell is "kind of" short and recognize that there is no definite demarcation between short and tall. We can state this mathematically as mSHORT(Russell) = 0.70, where m is the membership function.
Old Entry From; http://www.computerworld.com/The Probability Instinct
It looks as if Kant, who thought our minds structure our perceptions, was right. Probability was built into our minds. Our minds, the electrochemical symphony that our narrowly evolved neural ganglia play, impose an infrastructure on our thinking. The mind imposes a background of time and space and causal connectedness. Scientists have never seen a "causality" in the wild. They have seen, and they predict, only space-time events that follow space-time events. Apples on the tree, then apples in the air, then apples on the ground. Equations and correlations have replaced causes, just as science has largely replaced philosophy and religion as a theory of things. No causal germ in one event unfolds into another event. But the mind, as eighteenth-century philosopher David Hume observed, makes it seem so and inserts the causal links in the event chain.
Probability seems to be part of the same mental infrastructure. It forms part of our mental background or viewing screen along with time and space and causality and similarity and the topological notions of continuity and connectedness. We see probability everywhere because it lies in our glasses.
I believe that probability or "randomness" is a psychic instinct or Jungian archetype or mental trend that helps us organize our perceptions and memories and most of all our expectations. Probability gives structure to our competing causal predictions about how the future will unfold in the next instant or day or season or millennium.
Probability ranks or weights the future alternatives. Our expectations then blend or average these future alternatives into a single probability-weighted average. The probability weights do not exist outside our minds. They have no physical reality but have a powerful psychological reality rooted in our neural mi-crostructure. Hume also thought that we make up probability as we go and use it to fill in gaps in our mind schemes or world views: "Though there be no such thing as chance in the world, our ignorance of the real cause of any event has the same influence on the understanding and begets a like species of belief."
This probability instinct seems to cut across cultures and may cut across species. Besides the probability-laden psychology of scientists and most nonscientists, the widespread gambling and games of chance in primitive and modern cultures suggest that probability "reasoning" may be a cultural constant like hero worship or fertility rituals or incest and adultery taboos. A cultural constant suggests a biological substrate, and that requires an evolutionary history.
Ranking future alternatives can help pass on genes. Those who could so rank may have eaten those who could not. It allows us to bet before we act and improve the outcome of acting. That forward-looking ability has supreme survival value in biological evolution, the genetic variation and selection in the last few million years that has finely sculpted our brains and minds, and in the prior evolution that sculpted the brains and minds of our mammalian ancestors in the last 220 million years. Natural selection filters out organisms as they cross the fuzzy line from the present to the future. Natural selection favors brain mechanisms that help an organism make its next move in a changing and dangerous world. These forward-looking brain mechanisms may run deep in the structure of mammalian and even reptilian brains. Future studies may find that the brains of chimps and apes and lesser-brained mammals house a forward-looking probability instinct. At the other extreme we should not be surprised that scientists have exalted probability ranking into their grand organizing principle of maximum probability. Scientists follow their probability instincts as their hominid forefathers followed theirs. Scientists just know more math.
Fuzzy Thinking - The New Science of Fuzzy Logic - Bart Koskohttp://www.amazon.com/exec/obidos/tg/detail/-/078688021X/