almost a Newtonian system.
Since you can know the force imparted to the ball, and the mass of the ball, and you can calculate the angles at which it will strike the walls, you can predict the future behavior of the ball. In theory, you could predict the behavior of the ball far into the future, as it keeps bouncing from side to side. You could predict where it will end up three hours from now, in theory.
https://jurassicpark.fandom.com/wiki/Chaos_theory
In a scientific context, the word chaos has a slightly different meaning than it does in its general usage as a state of confusion, lacking any order. Chaos, with reference to chaos theory, refers to an apparent lack of order in a system that nevertheless obeys particular laws or rules; this understanding of chaos is synonymous with dynamical instability, a condition discovered by the physicist Henri Poincare in the early 20th century that refers to an inherent lack of predictability in some physical systems.
The two main components of chaos theory are the idea that systems - no matter how complex they may be - rely upon an underlying order, and that very simple or small systems and events can cause very complex behaviors or events. This latter idea is known as sensitive dependence on initial conditions, a circumstance discovered by Edward Lorenz (who is generally credited as the first experimenter in the area of chaos) in the early 1960s.
What is chaos theory?
https://whatis.techtarget.com/definition/chaos-theory
An Overview to Chaos Theory in Sociology
Chaos theory is a field of study in mathematics; however, it has applications in several disciplines, including sociology and other social sciences. In the social sciences, chaos theory is the study of complex non-linear systems of social complexity. It is not about disorder but rather about very complicated systems of order.
Nature, including some instances of social behavior and social systems, is highly complex, and the only prediction you can make is that it is unpredictable. Chaos theory looks at this unpredictability of nature and tries to make sense of it.
Chaos theory aims to find the general order of social systems and particularly social systems that are similar to each other. The assumption here is that the unpredictability in a system can be represented as overall behavior, which gives some amount of predictability, even when the system is unstable. Chaotic systems are not random systems. Chaotic systems have some kind of order, with an equation that determines overall behavior.
The first chaos theorists discovered that complex systems often go through a kind of cycle, even though specific situations are rarely duplicated or repeated. For example, say there is a city of 10,000 people. In order to accommodate these people, a supermarket is built, two swimming pools are installed, a library is erected, and three churches go up. In this case, these accommodations please everybody and equilibrium are achieved. Then a company decides to open a factory on the outskirts of town, opening jobs for 10,000 more people. The town then expands to accommodate 20,000 people instead of 10,000. Another supermarket is added, as are two more swimming pools, another library, and three more churches. The equilibrium is thus maintained. Chaos theorists study this equilibrium, the factors that affect this type of cycle, and what happens (what the outcomes are) when the equilibrium is broken.
Qualities of a Chaotic System
A chaotic system has three simple defining features:
Chaotic systems are deterministic. That is, they have some determining equation ruling their behavior.
Chaotic systems are sensitive to initial conditions. Even a very slight change in the starting point can lead to significantly different outcomes.
Chaotic systems are not random, nor disorderly. Truly random systems are not chaotic. Rather, chaos has a send of order and pattern.
Concepts
There are several key terms and concepts used in chaos theory:
Butterfly effect (also called sensitivity to initial conditions): The idea that even the slightest change in the starting point can lead to greatly different results or outcomes.
Attractor: Equilibrium within the system. It represents a state to which a system finally settles.
Strange attractor: A dynamic kind of equilibrium which represents some kind of trajectory upon which a system runs from situation to situation without ever settling down.
Applications in Real-Life
Chaos theory, which emerged in the 1970s, has impacted several aspects of real-life in its short life thus far and continues to impact all sciences. For instance, it has helped answer previously unsolvable problems in quantum mechanics and cosmology. It has also revolutionized the understanding of heart arrhythmias and brain function. Toys and games have also developed from chaos research, such as the Sim line of computer games (SimLife, SimCity, SimAnt, etc.).
By Ashley Crossman
Chaos Theory: A Brief Introduction
What exactly is chaos? The name "chaos theory" comes from the fact that the systems that the theory describes are apparently disordered, but chaos theory is really about finding the underlying order in apparently random data.
When was chaos first discovered? The first true experimenter in chaos was a meteorologist, named Edward Lorenz. In 1960, he was working on the problem of weather prediction. He had a computer set up, with a set of twelve equations to model the weather. It didn't predict the weather itself. However this computer program did theoretically predict what the weather might be.
One day in 1961, he wanted to
see a particular sequence again. To save time, he started in the middle of the sequence, instead
of the beginning. He entered the number off his printout and
left to let it run.
When he came back an hour later, the sequence had evolved differently. Instead of the same pattern as before, it diverged from the pattern, ending up wildly different from the original. (See figure 1.) Eventually he figured out what happened. The computer stored the numbers to six decimal places in its memory. To save paper, he only had it print out three decimal places. In the original sequence, the number was .506127, and he had only typed the first three digits, .506.
By all conventional ideas of the time, it should have worked. He should have gotten a sequence very close to the original sequence. A scientist considers himself lucky if he can get measurements with accuracy to three decimal places. Surely the fourth and fifth, impossible to measure using reasonable methods, can't have a huge effect on the outcome of the experiment. Lorenz proved this idea wrong.
This effect came to be known as the butterfly effect. The amount of difference in the starting points of the two curves is so small that it is comparable to a butterfly flapping its wings.
The flapping of a single butterfly's wing today produces a tiny change in the state of the atmosphere. Over a period of time, what the atmosphere actually does diverges from what it would have done. So, in a month's time, a tornado that would have devastated the Indonesian coast doesn't happen. Or maybe one that wasn't going to happen, does. (Ian Stewart, Does God Play Dice? The Mathematics of Chaos, pg. 141)
This phenomenon, common to chaos theory, is also known as sensitive dependence on initial conditions. Just a small change in the initial conditions can drastically change the long-term behavior of a system. Such a small amount of difference in a measurement might be considered experimental noise, background noise, or an inaccuracy of the equipment. Such things are impossible to avoid in even the most isolated lab. With a starting number of 2, the final result can be entirely different from the same system with a starting value of 2.000001. It is simply impossible to achieve this level of accuracy - just try and measure something to the nearest millionth of an inch!
From this idea, Lorenz stated that it is impossible to predict the weather accurately. However, this discovery led Lorenz on to other aspects of what eventually came to be known as chaos theory.
Lorenz started to look for a simpler system that had sensitive dependence on initial conditions. His first discovery had twelve equations, and he wanted a much more simple version that still had this attribute. He took the equations for convection, and stripped them down, making them unrealistically simple. The system no longer had anything to do with convection, but it did have sensitive dependence on its initial conditions, and there were only three equations this time. Later, it was discovered that his equations precisely described a water wheel.
At the top, water drips steadily into containers hanging on the wheel's rim. Each container drips steadily from a small hole. If the stream of water is slow, the top containers never fill fast enough to overcome friction, but if the stream is faster, the weight starts to turn the wheel. The rotation might become continuous. Or if the stream is so fast that the heavy containers swing all the way around the bottom and up the other side, the wheel might then slow, stop, and reverse its rotation, turning first one way and then the other. (James Gleick, Chaos - Making a New Science, pg. 29)
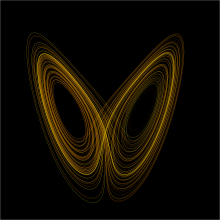
The equations for this system also seemed to give rise to entirely random behavior. However, when he graphed it, a surprising thing happened. The output always stayed on a curve, a double spiral. There were only two kinds of order previously known: a steady state, in which the variables never change, and periodic behavior, in which the system goes into a loop, repeating itself indefinitely. Lorenz's equations were definitely ordered - they always followed a spiral. They never settled down to a single point, but since they never repeated the same thing, they weren't periodic either. He called the image he got when he graphed the equations the Lorenz attractor. (See figure 2)
In 1963, Lorenz published a paper describing what he had discovered. He included the unpredictability of the weather, and discussed the types of equations that caused this type of behavior. Unfortunately, the only journal he was able to publish in was a meteorological journal, because he was a meteorologist, not a mathematician or a physicist. As a result, Lorenz's discoveries weren't acknowledged until years later, when they were rediscovered by others. Lorenz had discovered something revolutionary; now he had to wait for someone to discover him.
Another system in which sensitive dependence on initial conditions is evident is the flip of a coin. There are two variables in a flipping coin: how soon it hits the ground, and how fast it is flipping. Theoretically, it should be possible to control these variables entirely and control how the coin will end up. In practice, it is impossible to control exactly how fast the coin flips and how high it flips. It is possible to put the variables into a certain range, but it is impossible to control it enough to know the final results of the coin toss.
A similar problem occurs in ecology, and the prediction of biological populations. The equation would be simple if population just rises indefinitely, but the effect of predators and a limited food supply make this equation incorrect. The simplest equation that takes this into account is the following:
next year's population = r * this year's population * (1 - this year's population)
In this equation, the population is a number between 0 and 1, where 1 represents the maximum possible population and 0 represents extinction. R is the growth rate. The question was, how does this parameter affect the equation? The obvious answer is that a high growth rate means that the population will settle down at a high population, while a low growth rate means that the population will settle down to a low number. This trend is true for some growth rates, but not for every one.
One biologist, Robert May, decided to see what would happen to the equation as the growth rate value changes. At low values of the growth rate, the population would settle down to a single number. For instance, if the growth rate value is 2.7, the population will settle down to .6292. As the growth rate increased, the final population would increase as well. Then, something weird happened. As soon as the growth rate passed 3, the line broke in two. Instead of settling down to a single population, it would jump between two different populations. It would be one value for one year, go to another value the next year, then repeat the cycle forever. Raising the growth rate a little more caused it to jump between four different values. As the parameter rose further, the line bifurcated (doubled) again. The bifurcations came faster and faster until suddenly, chaos appeared. Past a certain growth rate, it becomes impossible to predict the behavior of the equation. However, upon closer inspection, it is possible to see white strips. Looking closer at these strips reveals little windows of order, where the equation goes through the bifurcations again before returning to chaos. This self-similarity, the fact that the graph has an exact copy of itself hidden deep inside, came to be an important aspect of chaos.
An employee of IBM, Benoit Mandelbrot was a mathematician studying this self-similarity. One of the areas he was studying was cotton price fluctuations. No matter how the data on cotton prices was analyzed, the results did not fit the normal distribution. Mandelbrot eventually obtained all of the available data on cotton prices, dating back to 1900. When he analyzed the data with IBM's computers, he noticed an astonishing fact:
The numbers that produced aberrations from the point of view of normal distribution produced symmetry from the point of view of scaling. Each particular price change was random and unpredictable. But the sequence of changes was independent on scale: curves for daily price changes and monthly price changes matched perfectly. Incredibly, analyzed Mandelbrot's way, the degree of variation had remained constant over a tumultuous sixty-year period that saw two World Wars and a depression. (James Gleick, Chaos - Making a New Science, pg. 86)
Mandelbrot analyzed not only cotton prices, but many other phenomena as well. At one point, he was wondering about the length of a coastline. A map of a coastline will show many bays. However, measuring the length of a coastline off a map will miss minor bays that were too small to show on the map. Likewise, walking along the coastline misses microscopic bays in between grains of sand. No matter how much a coastline is magnified, there will be more bays visible if it is magnified more.

One mathematician, Helge von Koch, captured this idea in a mathematical
construction called the Koch curve.
To create a Koch curve, imagine
an equilateral triangle.
To the middle third of each side, add another equilateral triangle. Keep on adding new triangles to the middle part of each side, and the result is a Koch curve. (See figure 4) A magnification of the Koch curve looks exactly the same as the original. It is another self-similar figure.
The Koch curve brings up an interesting paradox. Each time new triangles are added to the figure, the length of the line gets longer. However, the inner area of the Koch curve remains less than the area of a circle drawn around the original triangle. Essentially, it is a line of infinite length surrounding a finite area.
To get around this difficulty, mathematicians invented fractal dimensions. Fractal comes from the word fractional. The fractal dimension of the Koch curve is somewhere around 1.26. A fractional dimension is impossible to conceive, but it does make sense. The Koch curve is rougher than a smooth curve or line, which has one dimension. Since it is rougher and more crinkly, it is better at taking up space. However, it's not as good at filling up space as a square with two dimensions is, since it doesn't really have any area. So it makes sense that the dimension of the Koch curve is somewhere in between the two.
Fractal has come to mean any image that displays the attribute of self-similarity. The bifurcation diagram of the population equation is fractal. The Lorenz Attractor is fractal. The Koch curve is fractal.
During this time, scientists found it very difficult to get work published about chaos. Since they had not yet shown the relevance to real-world situations, most scientists did not think the results of experiments in chaos were important. As a result, even though chaos is a mathematical phenomenon, most of the research into chaos was done by people in other areas, such as meteorology and ecology. The field of chaos sprouted up as a hobby for scientists working on problems that maybe had something to do with it.
Later, a scientist by the name of Feigenbaum was looking at the bifurcation diagram again. He was looking at how fast the bifurcations come. He discovered that they come at a constant rate. He calculated it as 4.669. In other words, he discovered the exact scale at which it was self-similar. Make the diagram 4.669 times smaller, and it looks like the next region of bifurcations. He decided to look at other equations to see if it was possible to determine a scaling factor for them as well. Much to his surprise, the scaling factor was exactly the same. Not only was this complicated equation displaying regularity, the regularity was exactly the same as a much simpler equation. He tried many other functions, and they all produced the same scaling factor, 4.669.
This was a revolutionary discovery. He had found that a whole class of mathematical functions behaved in the same, predictable way. This universality would help other scientists easily analyze chaotic equations. Universality gave scientists the first tools to analyze a chaotic system. Now they could use a simple equation to predict the outcome of a more complex equation.
Many scientists were exploring equations that created fractal equations. The most famous fractal image is also one of the most simple. It is known as the Mandelbrot set (pictures of the mandelbrot set). The equation is simple: z=z2+c. To see if a point is part of the Mandelbrot set, just take a complex number z. Square it, then add the original number. Square the result, then add the original number. Repeat that ad infinitum, and if the number keeps on going up to infinity, it is not part of the Mandelbrot set. If it stays down below a certain level, it is part of the Mandelbrot set. The Mandelbrot set is the innermost section of the picture, and each different shade of gray represents how far out that particular point is. One interesting feature of the Mandelbrot set is that the circular humps match up to the bifurcation graph. The Mandelbrot fractal has the same self-similarity seen in the other equations. In fact, zooming in deep enough on a Mandelbrot fractal will eventually reveal an exact replica of the Mandelbrot set, perfect in every detail.
Fractal structures have been noticed in many real-world areas, as well as in mathematician's minds. Blood vessels branching out further and further, the branches of a tree, the internal structure of the lungs, graphs of stock market data, and many other real-world systems all have something in common: they are all self-similar.
Scientists at UC Santa Cruz found chaos in a dripping water faucet. By recording a dripping faucet and recording the periods of time, they discovered that at a certain flow velocity, the dripping no longer occurred at even times. When they graphed the data, they found that the dripping did indeed follow a pattern.
The human heart also has a chaotic pattern. The time between beats does not remain constant; it depends on how much activity a person is doing, among other things. Under certain conditions, the heartbeat can speed up. Under different conditions, the heart beats erratically. It might even be called a chaotic heartbeat. The analysis of a heartbeat can help medical researchers find ways to put an abnormal heartbeat back into a steady state, instead of uncontrolled chaos.
Researchers discovered a simple set of three equations that graphed a fern. This started a new idea - perhaps DNA encodes not exactly where the leaves grow, but a formula that controls their distribution. DNA, even though it holds an amazing amount of data, could not hold all of the data necessary to determine where every cell of the human body goes. However, by using fractal formulas to control how the blood vessels branch out and the nerve fibers get created, DNA has more than enough information. It has even been speculated that the brain itself might be organized somehow according to the laws of chaos.
Chaos even has applications outside of science. Computer art has become more realistic through the use of chaos and fractals. Now, with a simple formula, a computer can create a beautiful, and realistic tree. Instead of following a regular pattern, the bark of a tree can be created according to a formula that almost, but not quite, repeats itself.
Music can be created using fractals as well. Using the Lorenz attractor, Diana S. Dabby, a graduate student in electrical engineering at the Massachusetts Institute of Technology, has created variations of musical themes. ("Bach to Chaos: Chaotic Variations on a Classical Theme", Science News, Dec. 24, 1994) By associating the musical notes of a piece of music like Bach's Prelude in C with the x coordinates of the Lorenz attractor, and running a computer program, she has created variations of the theme of the song. Most musicians who hear the new sounds believe that the variations are very musical and creative.
Chaos has already had a lasting effect on science, yet there is much still left to be discovered. Many scientists believe that twentieth century science will be known for only three theories: relativity, quantum mechanics, and chaos. Aspects of chaos show up everywhere around the world, from the currents of the ocean and the flow of blood through fractal blood vessels to the branches of trees and the effects of turbulence. Chaos has inescapably become part of modern science. As chaos changed from a little-known theory to a full science of its own, it has received widespread publicity. Chaos theory has changed the direction of science: in the eyes of the general public, physics is no longer simply the study of subatomic particles in a billion-dollar particle accelerator, but the study of chaotic systems and how they work.
This article presents the major historical steps In the acquisition of knowledge in physics that led to chaos theory Since these steps were made in fields other than biology or medicine, these will be referred to, in particular astronomy. Some readers might not be familiar with physics or mathematics; therefore explanations using the language of equations have been kept to a minimum.
Definitions of concepts related to the history of chaos theory.*
Causality principle. Every effect has an antecedent proximate cause.
Determinism. A philosophical proposition that every event is physically determined by an unbroken chain of prior occurrences.
Predictability. This refers to the degree that a correct forecast of a system's state can be made either qualitatively or quantitatively
Model. A pattern, plan, representation, or description designed to show the structure or workings of an object, System, or concept.
Dynamical system. A System that changes over time in both a causal and a deterministic manner; ie, its future depends only on phenomena from its past and its present (causality) and each given initial condition will lead to only one given later state of the System (determinism). Systems that are noisy or stochastic, in the sense of showing randomness, are not dynamical Systems, and the probability theory is the one to apply to their analysis.
Phase space. An abstract space in which ail possible states of a System are represented which, each possible state of the System corresponding to one unique point in the phase space.
Sensitivity to initial conditions. This is when a change in one variable has the consequence of an exponential change in the system.
Integrable system. In mathematics, this refers to a System of differential equations for which solutions can be found. In mechanics, this refer to a system that is quasiperiodic.
Linear System. A system is said to be linear when the whole is exactly equal to the sum of its components, Attractor» A set to which a dynamical System evolves after a long enough time.
Characteristic Lyapynov time. The characteristic time of a system is defined as the delay when changes from the initial point are multiplied by 10 in the phase space.
Feedback. A response to information, that either increases effects (positive feedback), or decreases them (negative feedback), or induces a cyclic phenomenon.
Self-similarity. This means that an object is composed of subunits and sub subunits on multiple levels that (statistically) resemble the structure of the whole object, However; in every day life, there are necessarily lower and upper boundaries over which such self-similar behavior applies.
Fractal. Is a geometrical object satisfying two criteria: self-similarity and fractional dimensionality.
Fractal dimension. Let an object in a n-dimensions space be covered by the smallest number of open spheres of radius r. The fractal dimension is log(N)/log(1/r) when r tends towards 0.
Some of the terms are used with different meanings in fields other than physics. For example, the adjective linear pharmacokinetics describes a body clearance of a constant fraction per unit of time of the total amount of a substance in the body while a nonlinear pharmacokinetics describes the elimination of a constant quantity of cormpound per unit of time. AIso feedback is a well-known term in biology or medicine, while its use in physics is less familiar to nonphysicists.
A History of Chaos Theory
https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3202497/
Chaos Theory
Chaos theory is a branch of mathematics focusing on the study of chaos — dynamical systems whose apparently random states of disorder and irregularities are actually governed by underlying patterns and deterministic laws that are highly sensitive to initial conditions.[1][2] Chaos theory is an interdisciplinary theory stating that, within the apparent randomness of chaotic complex systems, there are underlying patterns, interconnectedness, constant feedback loops, repetition, self-similarity, fractals, and self-organization.[3] The butterfly effect, an underlying principle of chaos, describes how a small change in one state of a deterministic nonlinear system can result in large differences in a later state (meaning that there is sensitive dependence on initial conditions).[4] A metaphor for this behavior is that a butterfly flapping its wings in Texas can cause a hurricane in China.[5]
Small differences in initial conditions, such as those due to errors in measurements or due to rounding errors in numerical computation, can yield widely diverging outcomes for such dynamical systems, rendering long-term prediction of their behavior impossible in general.[6] This can happen even though these systems are deterministic, meaning that their future behavior follows a unique evolution[7] and is fully determined by their initial conditions, with no random elements involved.[8] In other words, the deterministic nature of these systems does not make them predictable.[9][10] This behavior is known as deterministic chaos, or simply chaos. The theory was summarized by Edward Lorenz as:[11]
Chaotic behavior exists in many natural systems, including fluid flow, heartbeat irregularities, weather and climate.[12][13][7] It also occurs spontaneously in some systems with artificial components, such as the stock market and road traffic.[14][3] This behavior can be studied through the analysis of a chaotic mathematical model, or through analytical techniques such as recurrence plots and Poincaré maps. Chaos theory has applications in a variety of disciplines, including meteorology,[7] anthropology,[15] sociology,[16][ environmental science, computer science, engineering, economics, ecology, pandemic crisis management,[17][18] and philosophy. The theory formed the basis for such fields of study as complex dynamical systems, edge of chaos theory, and self-assembly processes.
Chaos
The big news about chaos is supposed to be that the smallest of changes in a system can result in very large differences in that system’s behavior. The so-called butterfly effect has become one of the most popular images of chaos. The idea is that the flapping of a butterfly’s wings in Argentina could cause a tornado in Texas three weeks later. By contrast, in an identical copy of the world sans the Argentinian butterfly, no such storm would have arisen in Texas. The mathematical version of this property is known as sensitive dependence. However, it turns out that sensitive dependence is somewhat old news, so some of the implications flowing from it are perhaps not such “big news” after all. Still, chaos studies have highlighted these implications in fresh ways and led to thinking about other implications as well.
In addition to exhibiting sensitive dependence, chaotic systems possess two other properties: they are deterministic and nonlinear (Smith 2007). This entry discusses systems exhibiting these three properties and what their philosophical implications might be for theories and theoretical understanding, confirmation, explanation, realism, determinism, free will and consciousness, and human and divine action.
- 1. Defining Chaos: Determinism, Nonlinearity and Sensitive Dependence
- 2. What is Chaos “Theory”?
- 3. Nonlinear Models, Faithfulness and Confirmation
- 4. Chaos, Determinism and Quantum Mechanics
- 5. Questions about Realism and Explanation
- 6. Quantum Chaos
- 7. Some Broader Implications of Chaos
- 8. Conclusion
- Appendix: Global Lyapunov Exponents
- Bibliography
- Academic Tools
- Other Internet Resources
- Related Entries